Optical coherence is one of the most fundamental concepts in modern optics. It’s the theoretical foundation for understanding how light waves interact and interfere. This phenomenon decides if light sources can make stable interference patterns—directly affecting applications like precision measurements and advanced imaging.
At its core, coherence describes how well electromagnetic waves keep predictable phase relationships across space and time. It sets highly ordered laser light apart from chaotic emissions of everyday sources, like incandescent bulbs.
Optical coherence means having a fixed phase relationship between electric field values at different spatial locations or times in a light field. When light waves keep this consistent phase relationship, they can make stable interference effects you can observe and measure. This property decides if two or more light waves can interfere constructively or destructively in a predictable way.
The math behind coherence uses correlation functions to measure the phase relationship between different points in an electromagnetic field. For a light field to be coherent, it needs to meet specific conditions: its waves must have the same frequency, keep consistent vibration directions, and have constant phase differences between them.
When two coherent waves meet, their interference pattern depends a lot on their relative phase difference. Constructive interference happens when waves arrive in phase—peaks and troughs line up—making amplitude bigger. Conversely, destructive interference happens when waves are out of phase—peaks meet troughs—so amplitude gets smaller or disappears.
For waves to be "perfectly coherent," their phase difference must stay constant over time. Math-wise, this needs identical frequencies. At the other end, "completely incoherent" waves—like those from thermal sources (incandescent lamps, the sun)—have rapidly changing phase relationships. This stops stable interference patterns from forming. Between these extremes is "partially coherent" light. It includes most practical light sources and has intermediate interference abilities.
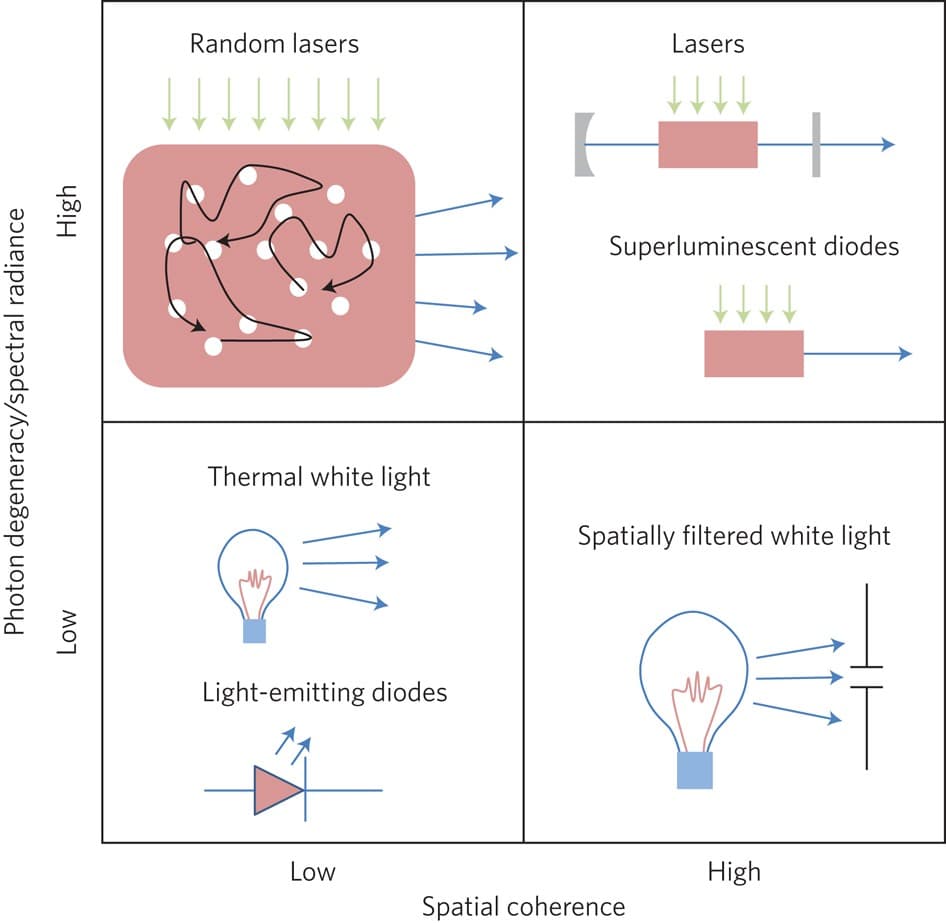
Different light sources are categorized by their coherence properties—from highly incoherent thermal sources to ultra-coherent laser systems. This classification directly affects their practical uses and decides which optical techniques work.
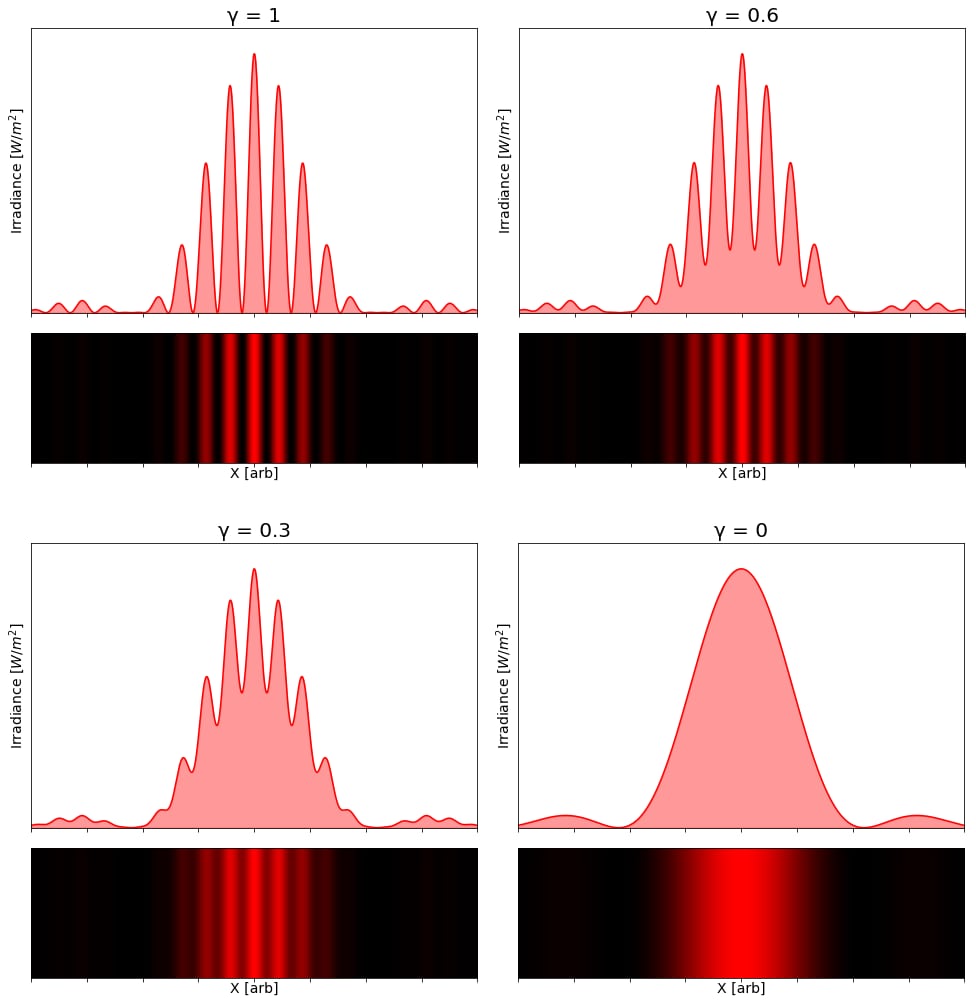
Optical coherence shows up in two distinct but complementary ways: spatial coherence (phase relationships across the beam's cross-section) and temporal coherence (phase consistency over time).
Spatial coherence measures the correlation between electric field values at different transverse positions in a light beam's cross-section. This property decides how well the phase relationship stays across the beam's spatial extent. It directly affects how well light keeps its shape and direction as it travels.
In lasers with diffraction-limited beam quality, electric fields at different spatial locations oscillate in perfect correlation. This is true even if the temporal structure has complex superpositions of multiple frequency components. This high spatial coherence lets laser beams have their characteristic strong directionality—and lets them focus to extremely small spots.
A light source's spatial coherence is closely tied to its apparent size and the distance from which you observe it. The van Cittert-Zernike theorem says thermal sources (like stars) can have significant spatial coherence when observed from far enough away—even though they're intrinsically incoherent.
Temporal coherence describes the correlation between electric field values at a single spatial location but at different times. This property directly ties to the monochromaticity of the light source—how close its emission is to a single, pure frequency.
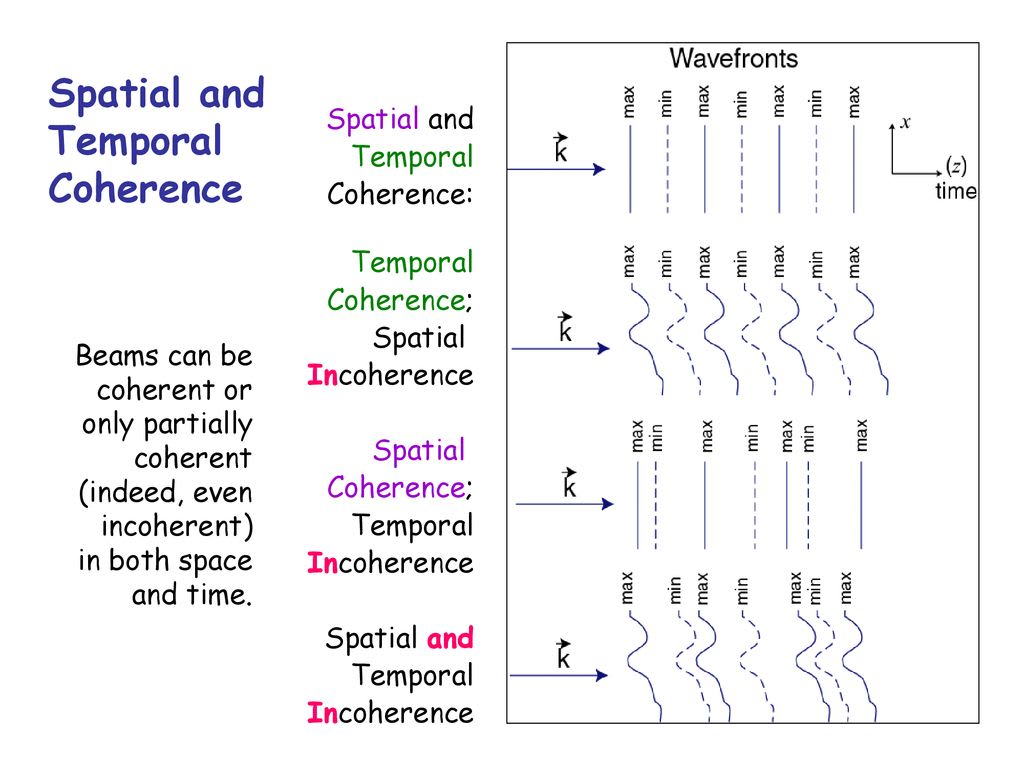
Single-frequency lasers are a good example of high temporal coherence. They make clean sinusoidal oscillations that stay predictable over long periods. You can measure temporal coherence using coherence time (τc)—the time the phase stays predictable—and coherence length (Lc)—the distance light travels during that time.
The link between spectral properties and temporal coherence follows well-known math principles. Coherence time is inversely proportional to spectral linewidth: τc = 1/Δν (Δν is frequency bandwidth). Similarly, coherence length is Lc = c × τc = c/Δν (c is speed of light).
For sources with Gaussian spectral distributions, coherence length is Lc = λ²/(2Δλ) (λ is center wavelength, Δλ is spectral width). These relationships let you predict coherence properties from easily measured spectral characteristics.
When coherent light interacts on optical elements, it shows important things about coherence behavior. When a spatially coherent laser beam goes through an optical diffuser, the diffuser disrupts the wavefront but might keep the underlying phase relationships.
If the diffuser stays still, the distorted beam that results can still be considered spatially coherent on principle. The phase relationships between different points stay fixed—even though they're complex. However, true disruption of spatial coherence needs time-varying wavefront distortions—like those from a rotating diffuser. In these cases, spatial coherence gets worse but temporal coherence might stay the same. This shows that these two aspects of coherence are independent.
Highly coherent laser light makes characteristic speckle patterns when it reflects on rough surfaces. These granular intensity patterns come from the interference of many coherent wavelets scattered from different points on the surface. The statistical properties of speckle patterns tell you valuable things about the coherence properties of the light that's illuminating the surface.
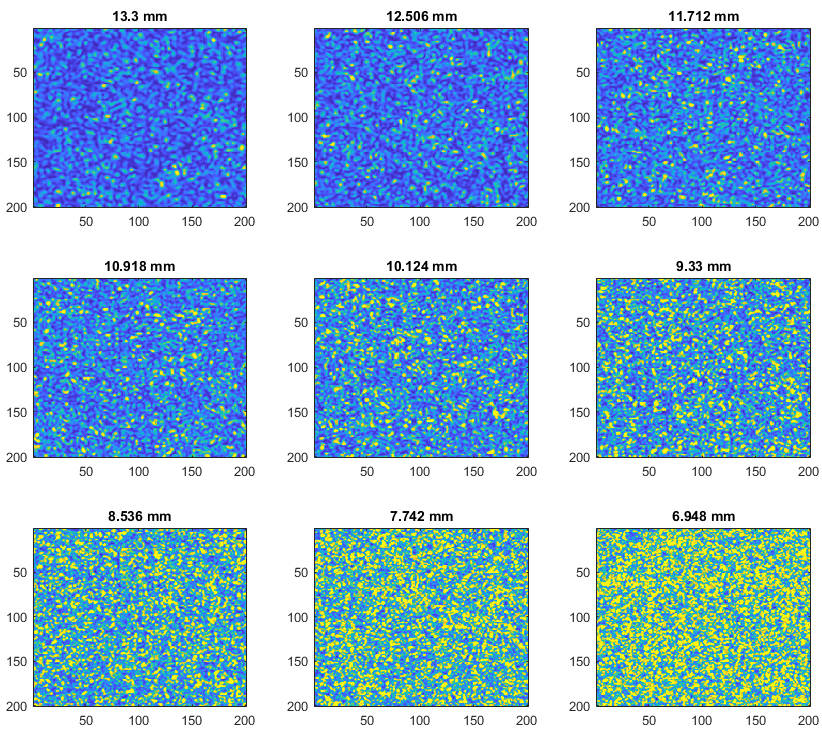
How visible and what speckle patterns look like depend a lot on the spatial and temporal coherence of the light source. Sources with longer coherence lengths make more obvious speckle effects. Partially coherent sources can reduce speckle contrast—so they're better for some imaging applications.
Lasers get their remarkable spatial coherence from resonator modes—patterns that define spatially correlated fields. This is probably the most fundamental difference between laser radiation and conventional light sources. The resonator's shape and the gain medium's properties decide the specific mode structure—and thus the spatial coherence characteristics.
Different laser setups make different degrees of spatial coherence. Single-mode lasers running in fundamental Gaussian modes have the highest spatial coherence. This lets them be used in applications that need precise beam shaping and focusing. Multimode lasers keep good spatial coherence but support multiple transverse modes. These modes can lower the overall coherence quality.
How temporally coherent a laser system is depends a lot on how it's operated. Single longitudinal mode operation—where only one resonator mode has enough gain to oscillate—makes exceptionally high temporal coherence. Advanced stabilization techniques can make linewidths extremely small. Some optical frequency standards have linewidths below 1 Hz—coherence lengths over hundreds of thousands of kilometers.
On the other hand, multimode laser operation uses multiple longitudinal modes with different frequencies. This makes temporal coherence lower. Even single-frequency lasers can have poor temporal coherence because of phase noise—especially in semiconductor laser diodes.
Mode-locked lasers for ultrashort pulse generation are a unique case. The link between optical bandwidth and temporal coherence gets complex here. These systems can have both broad spectral bandwidths and high temporal coherence at the same time. The Fourier spectrum has discrete, narrow spectral lines that form frequency combs. This lets them have high temporal coherence for time delays close to integer multiples of the pulse period.
Different optical applications need specific coherence properties. This decides which light source is right. Interferometric measurements usually need high temporal coherence to keep interference visible over large path differences. Holographic recording needs both high spatial and temporal coherence to capture and reconstruct 3D information accurately. Optical coherence tomography (OCT) uses controlled coherence properties to get high-resolution biomedical imaging. These systems usually use superluminescent diodes with broad spectral bandwidths. This lets them get micrometer-scale axial resolution while keeping enough spatial coherence for effective light delivery and collection.
Measuring coherence usually uses interferometric techniques that directly probe correlation functions. Time-domain methods measure how visible interference is as path difference changes. Frequency-domain methods analyze spectral properties to figure out coherence characteristics.
Advanced techniques let you measure spatial coherence in a single shot using specially designed aperture arrays. These methods are especially useful for characterizing sources that vary from shot to shot—like high-harmonic generation sources and X-ray free-electron lasers.
Modern optical systems more and more need coherence properties tailored for specific applications. Spatial coherence engineering lets you reduce speckle effects in display systems while keeping enough coherence for effective light delivery. Tunable coherence sources let you dynamically optimize imaging and processing conditions.
Optical coherence is a fundamental property that links theoretical optics to practical applications. The difference between spatial and temporal coherence gives a framework for understanding and optimizing light sources for specific applications. From highly coherent stabilized lasers (used for precision measurements) to controlled partially coherent biomedical imaging systems, understanding coherence principles is still key to advancing optical technologies.
Coherence-based applications keep developing—from quantum optical systems to advanced manufacturing processes. This shows how important these fundamental concepts still are. As optical technologies keep evolving, coherence principles will definitely stay central to innovations in fields like telecommunications, metrology, medicine, and materials processing.
Contact: Jason
Phone: +8613337332946
E-mail: [email protected]
Add: Hangzhou City, Zhejiang Province, China