Quantum mechanics describes atomic systems in ways that break sharply with classical ideas about energy and measurement. Introductory courses often say atomic energy levels are perfectly discrete. But quantum mechanics shows reality is more complex.
Natural linewidth comes from the uncertainty principle—a fundamental quantum rule. It turns our idea of atomic transitions from perfect single-frequency emissions to complex spectroscopic effects with built-in broadening. These quantum details matter a lot for atomic spectroscopy, laser physics, and precision metrology.
Excited atomic states don’t last forever. Quantum mechanics sets limits on them. Together, they make spectral lines wider—lines we can measure to learn about atomic structure and how atoms behave. To understand these effects, we need to leave simple models behind. We have to accept that quantum systems are probabilistic—and that this affects what we can observe.
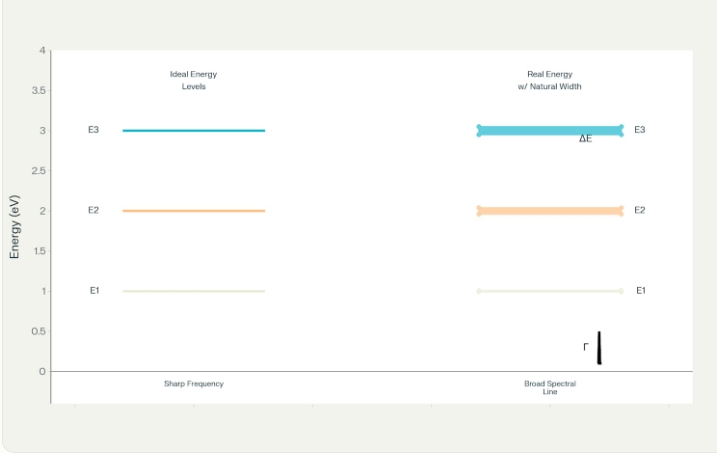
Traditional atomic models showed energy levels as infinitely sharp lines between quantum states. People thought transitions would make perfectly single-color radiation—with frequency ν = (E₂ - E₁)/h. This idealized view helps teach, but it clashes with how quantum mechanics works—probabilistically—and with Heisenberg's uncertainty principle.
Heisenberg's energy-time uncertainty relation is the theory behind natural linewidth:
ΔE · Δt ≥ ℏ/2
Here, ΔE is how uncertain we are about energy. Δt is how long a quantum state lasts. ℏ is the reduced Planck constant. The position-momentum uncertainty relation is different. The time-energy one uses time as a parameter, not something we can observe directly. This makes it trickier to interpret—but just as important.
![]()
For atomic energy levels, Δt (time uncertainty) is exactly the average lifetime of an excited state. That’s how long an atom stays at a certain energy level before dropping to a lower one. This link turns the abstract uncertainty principle into something real—something we can measure in spectroscopy.
Natural linewidth (Γ) of an energy level follows this equation:
Γ = ℏ/τ = 1/(2πτ)
Here, τ is the state’s lifetime. This means a simple inverse relationship: shorter lifetimes make broader spectral lines. Longer-lived states make narrower ones.
Different atomic states have very different lifetimes—and very different natural linewidths. This makes a hierarchy of how they behave in spectroscopy.
Excited States: They last about a nanosecond. This makes natural linewidths of tens to hundreds of megahertz. They emit light quickly through allowed electric dipole transitions.
Metastable States: They last from microseconds to milliseconds. Their natural linewidths are narrow. Why? Quantum selection rules slow their decay. Their transitions to lower states are "forbidden." This is because symmetry rules block the usual dipole interactions that cause decay.
Ground States: Under perfect conditions, they last forever. Their natural linewidth is zero. This makes them stable references for spectroscopy.
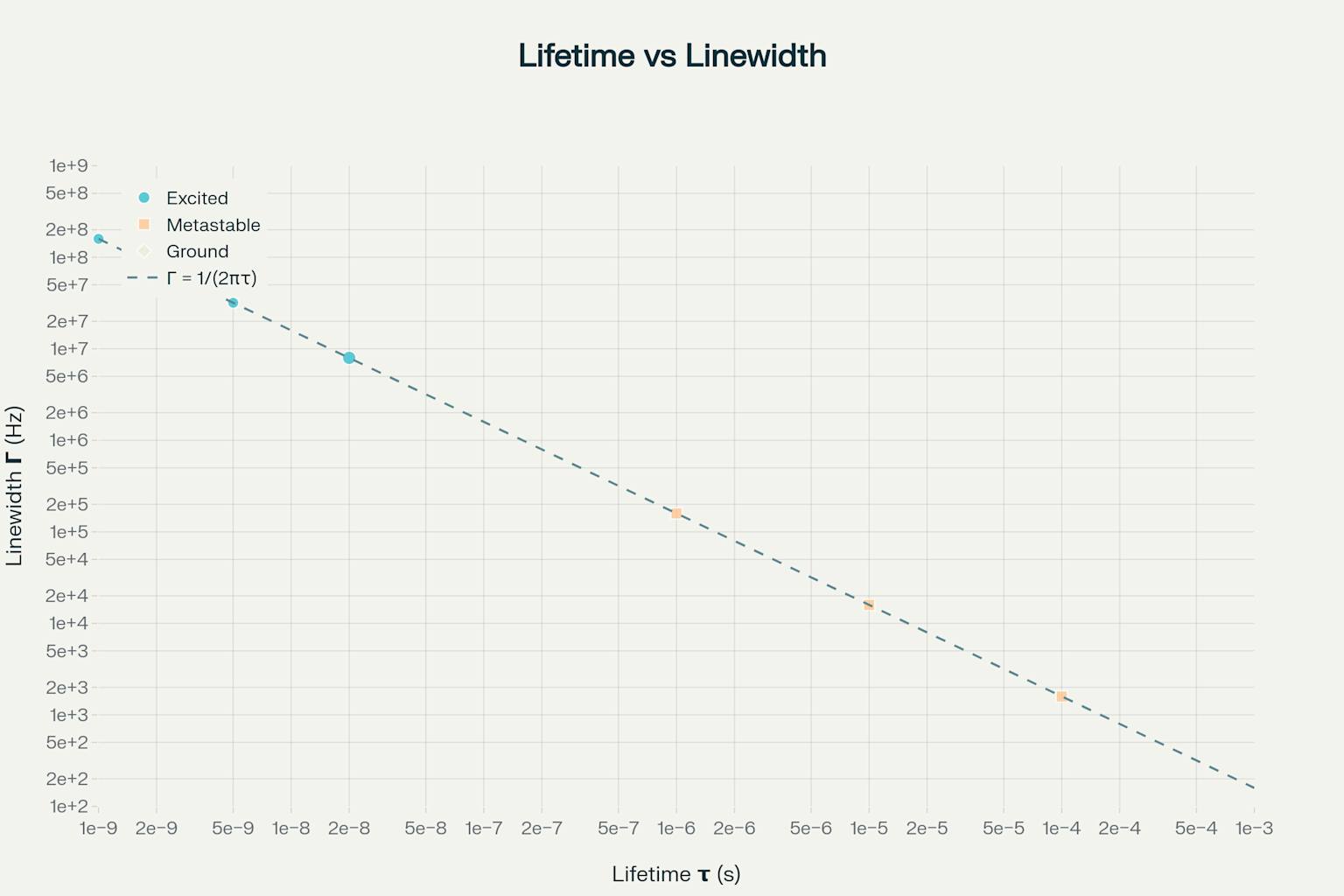
Lifetime and natural linewidth are linked across many orders of magnitude. Atomic physics gives us specific examples. An typical excited state lasts 1 nanosecond. Its natural linewidth is about 160 MHz. A metastable state lasts a microsecond. Its linewidth is just 160 kHz.
This big difference matters a lot for different uses. Atomic clocks use narrow transitions from long-lived metastable states to stay stable. Laser systems have to balance two things: enough gain (needs shorter lifetimes) and pure spectral lines (needs longer lifetimes).
Natural linewidth is a fundamental quantum limit. But it’s usually just one of many things that make spectral lines wider. In most experiments, these are the main things that widen lines:
Doppler Broadening (~1 GHz): Comes from atoms moving thermally. It’s the biggest factor at room temperature.
Collisional Broadening (~100 MHz): Happens when atoms collide. This stops the emission process.
Natural Broadening (~10 MHz): The quantum limit you can’t get rid of.
Instrumental Broadening (variable): Depends on how good your spectrometer is and your optical parts.
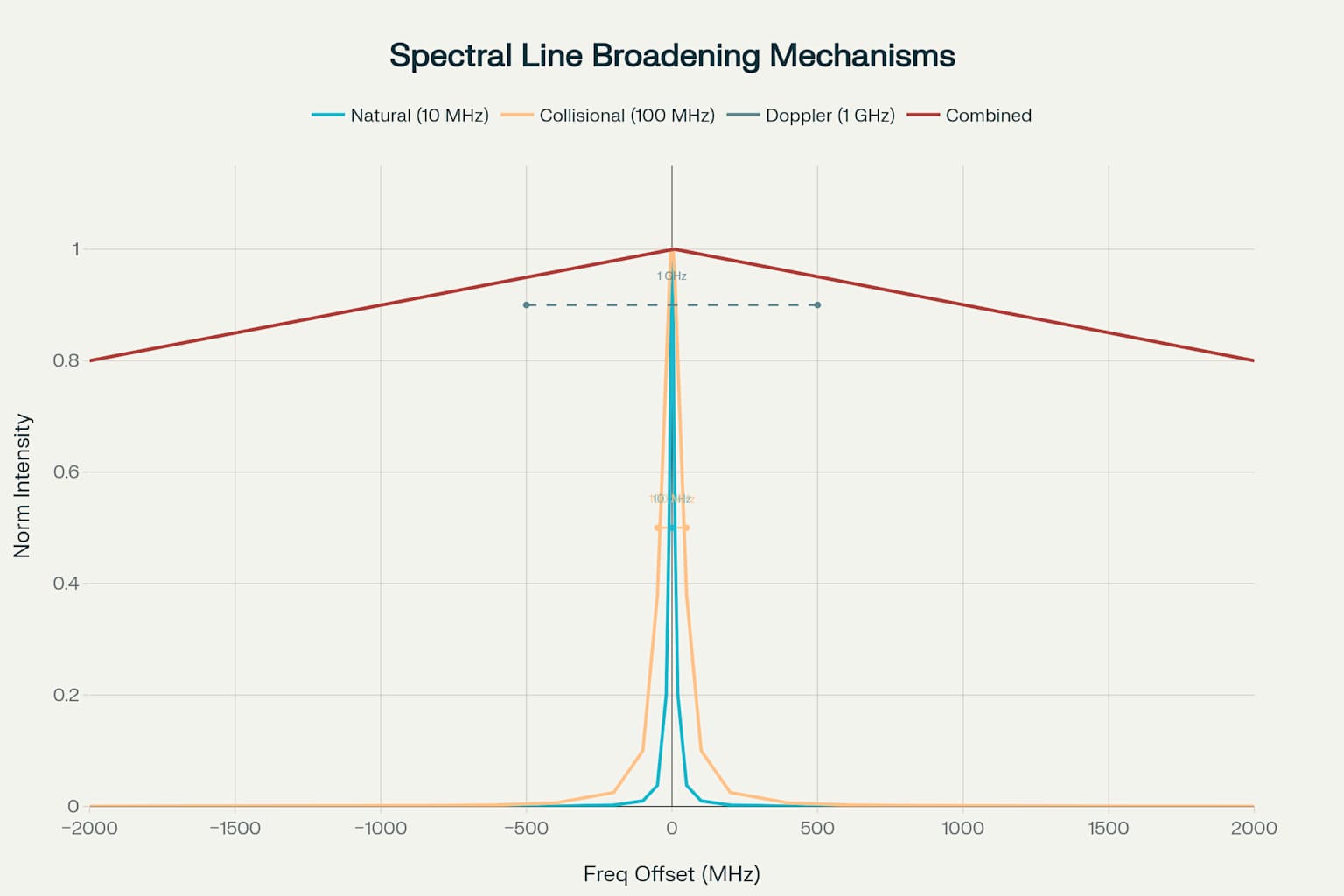
Natural broadening makes a Lorentzian lineshape. It follows this equation:
I(ν) = I₀ · [Γ/2π] / [(ν - ν₀)² + (Γ/2π)²]
Here, I₀ is peak intensity. ν₀ is center frequency. Γ is natural linewidth. Lorentzian profiles have wider "wings" than Gaussian ones. This comes from excited states decaying exponentially—and from quantum mechanics.
When different broadening mechanisms mix, they make complex lineshapes. We can analyze these to learn about atoms, the environment, and our tools.
The helium-neon laser is a great example of how natural linewidth works in real life. Its famous 632.8 nm light comes from a transition on neon atoms—between the 5s² upper level and 3p⁴ lower level. The measurements here show the principles we talked about.
Upper Level: The 5s² state lasts about 20 nanoseconds. That means a natural linewidth of 8.0 MHz. This is a long lifetime for an excited state. It’s because the upper laser level is metastable—which makes the laser more efficient.
Lower Level: The 3p⁴ state lasts about 100 nanoseconds. Its natural linewidth is 1.6 MHz. This level decays faster. That helps keep population inversion on the laser medium.
Total Linewidth: The total natural linewidth of the transition comes from both levels. It’s about 9.6 MHz. This narrow linewidth explains why He-Ne lasers have such good coherence.
Modern spectroscopy lets us see natural linewidth directly—if we control the conditions carefully. Beam-foil spectroscopy and electron beam ion trap (EBIT) methods measure atomic lifetimes—from nanoseconds to milliseconds. This gives us data to test theories.
To measure natural linewidth, we need to get rid of other broadening mechanisms—or account for them carefully. That usually means: working on low pressures to reduce collisional effects, using laser cooling to cut down on Doppler broadening, and using high-resolution spectrometers to minimize instrumental broadening.
Understanding natural linewidth is key for many uses in modern physics and technology.
Precision Metrology: Atomic frequency standards use narrow natural linewidths to get super accurate timing. This helps with GPS satellites and fundamental physics tests.
Quantum Optics: How atoms interact with electromagnetic fields depends on the ratio of natural linewidth to other energy scales. This affects things like cavity quantum electrodynamics and quantum information processing.
Plasma Diagnostics: In hot plasmas, natural linewidth tells us about atomic level populations and transition rates. This is key on fusion energy research and astrophysics.
Laser Development: To optimize laser systems, you need to understand natural linewidth—and how it links to gain, threshold conditions, and output.
Natural linewidth shows how quantum mechanics links to things we can measure. Heisenberg's energy-time uncertainty relation is often seen as an abstract idea. But it shows up directly in atomic spectroscopy—and affects precision measurements and technology.
Studying natural linewidth also tells us about how measurement works in quantum mechanics. We can’t measure energy and time perfectly at the same time. This reflects how quantum phenomena are probabilistic—and how measurement always disturbs what we’re looking at.
As experiments get more precise, the fundamental limits of natural linewidth matter more and more. Today’s research on optical atomic clocks is getting so precise that natural linewidth is a big constraint. This pushes the limits of what we can do with quantum mechanics.
New spectroscopy methods and laser systems get better because we understand natural linewidth—and how to optimize it for specific uses. This includes ultranarrow laser systems, precision spectroscopy of exotic atoms, and quantum-enhanced measurements.
Moving from idealized atomic energy levels to the quantum reality of natural linewidth shows how fundamental physics principles affect what we can see. Classical ideas say atomic transitions should make perfectly sharp spectral lines. But quantum mechanics tells us: excited states don’t last forever—so all atomic emissions are wider.
This broadening is often small compared to environmental effects. But it’s a limit we can’t get rid of—set by the uncertainty principle and quantum probability. Understanding natural linewidth doesn’t just help us appreciate quantum phenomena. It’s also the foundation for better precision measurements, laser technology, and quantum applications.
The helium-neon laser example shows: even in well-optimized systems, quantum constraints still affect what we observe. As experiments get better and new uses emerge, the principles behind natural linewidth will still be key to understanding atomic physics and its tech applications.
Studying natural linewidth bridges fundamental quantum mechanics and practical spectroscopy. It shows how abstract theories become measurable phenomena—phenomena that change how we understand nature and build advanced tech. This link between theory and application shows why quantum mechanics still matters in today’s science and engineering.
Contact: Jason
Phone: +8613337332946
E-mail: [email protected]
Add: Hangzhou City, Zhejiang Province, China