Relaxation oscillations are one of most fascinating & practically important phenomena on laser physics. They fundamentally affect stability, performance, and control of modern laser systems. These oscillatory behaviors come from intricate coupling between laser power and gain mechanisms. They create distinctive patterns that distinguish different classes of lasers and influence their applications across industries—from telecommunications to medical diagnostics.
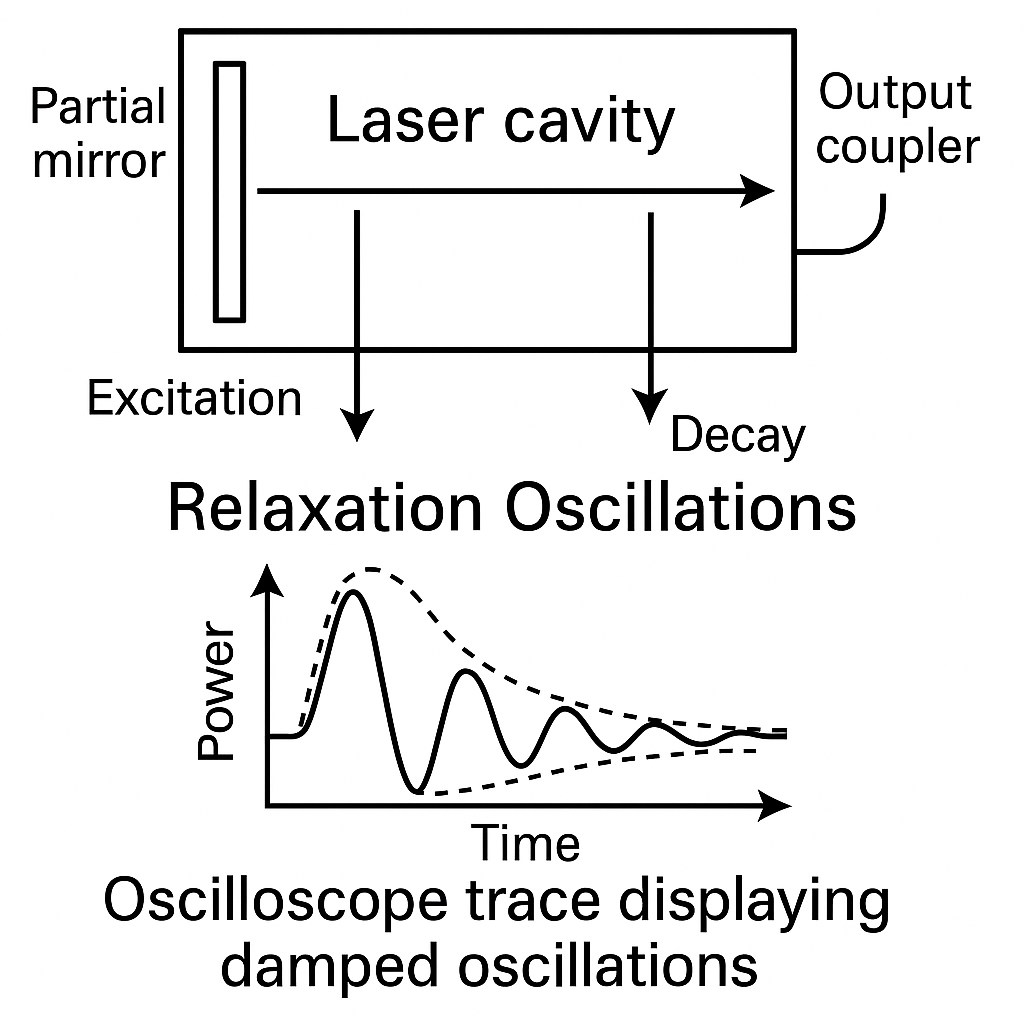
Relaxation oscillations are small - amplitude, mutually coupled oscillations of laser power and laser gain around their steady - state equilibrium values. When a laser meets disturbances during operation—like fluctuations in pump power, mechanical vibrations, or thermal variations—the output power doesn’t immediately return to its steady state. Instead, it shows characteristic oscillatory behavior before finally stabilizing.
The fundamental nature of these oscillations comes from finite response time of gain medium compared to photon dynamics within laser cavity. Unlike simple harmonic oscillations, relaxation oscillations are inherently nonlinear. They show exponential damping characteristics that depend on specific laser parameters and operating conditions.
The occurrence and characteristics of relaxation oscillations depend critically on relationship between two fundamental timescales: upper - state lifetime of gain medium and cavity damping time. This relationship forms basis for classifying lasers into distinct operational regimes that determine their dynamic behavior.
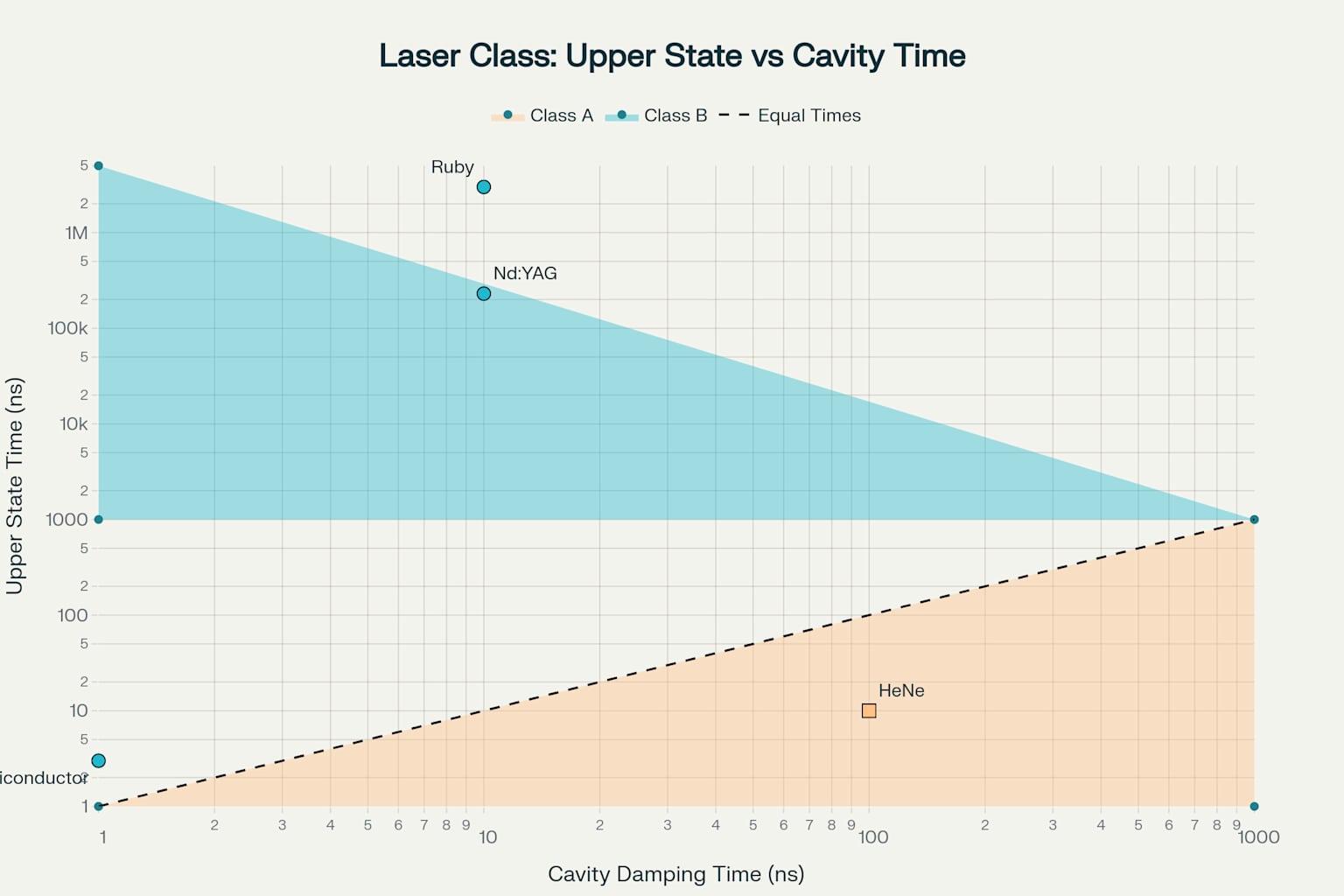
Class A lasers operate in an regime where upper - state lifetime is significantly shorter than cavity damping time. In this configuration, gain medium can respond rapidly to changes in intracavity photon population, effectively following instantaneous photon dynamics. Gas lasers such as helium - neon and carbon dioxide lasers typically operate in this regime. They show smooth exponential approaches to steady - state operation without oscillatory behavior.
Class B lasers are characterized by upper - state lifetimes that exceed cavity damping time by substantial margins. This temporal mismatch creates an fundamental instability in system dynamics. The gain medium can’t respond quickly enough to changes in photon population, leading to characteristic relaxation oscillations. Most practical laser systems, including solid - state lasers, semiconductor diodes, and rare - earth - doped fiber lasers, operate in this regime.
The underlying physics of relaxation oscillations can be understood through coupled rate equations that govern photon and carrier populations within laser system. The mechanism involves complex interplay between stimulated emission, spontaneous emission, and population dynamics that creates self - sustained oscillatory behavior.
When pump power is suddenly applied to an Class B laser, the system goes through an predictable sequence of events. Initially, population inversion builds up in gain medium as excited carriers accumulate faster than they can be depleted through spontaneous emission. Once gain exceeds cavity losses, stimulated emission begins to dominate. It rapidly depletes stored energy and creates an intense output pulse or “spike”.
The depletion of gain medium reduces available population inversion below steady - state level, causing photon population to decay. As pump continues to operate, population inversion gradually rebuilds. But the depleted state means the system overshoots in opposite direction. This creates an feedback loop that manifests as damped oscillations around equilibrium operating point.
The frequency of relaxation oscillations is determined by fundamental laser parameters including intracavity power, resonator losses, round - trip time, saturation energy, and upper - state lifetime. For Class B lasers, relaxation oscillation frequency follows well - established scaling relationships that enable precise prediction and control.
For solid - state lasers operating well above threshold, relaxation oscillation frequency approximately follows the relationship: f_RO ≈ (1/2π) × √(ρP_int / T_rt E_sat), where ρ represents resonator losses, P_int is intracavity power, T_rt is round - trip time, and E_sat is saturation energy. This relationship shows that oscillation frequency increases with square root of pump power above threshold.
Different laser types show characteristic frequency ranges that reflect their underlying physical properties. Solid - state lasers such as Nd:YAG typically show relaxation oscillations in kilohertz range, while semiconductor lasers exhibit much higher frequencies in gigahertz region due to their shorter carrier lifetimes and smaller cavity volumes.
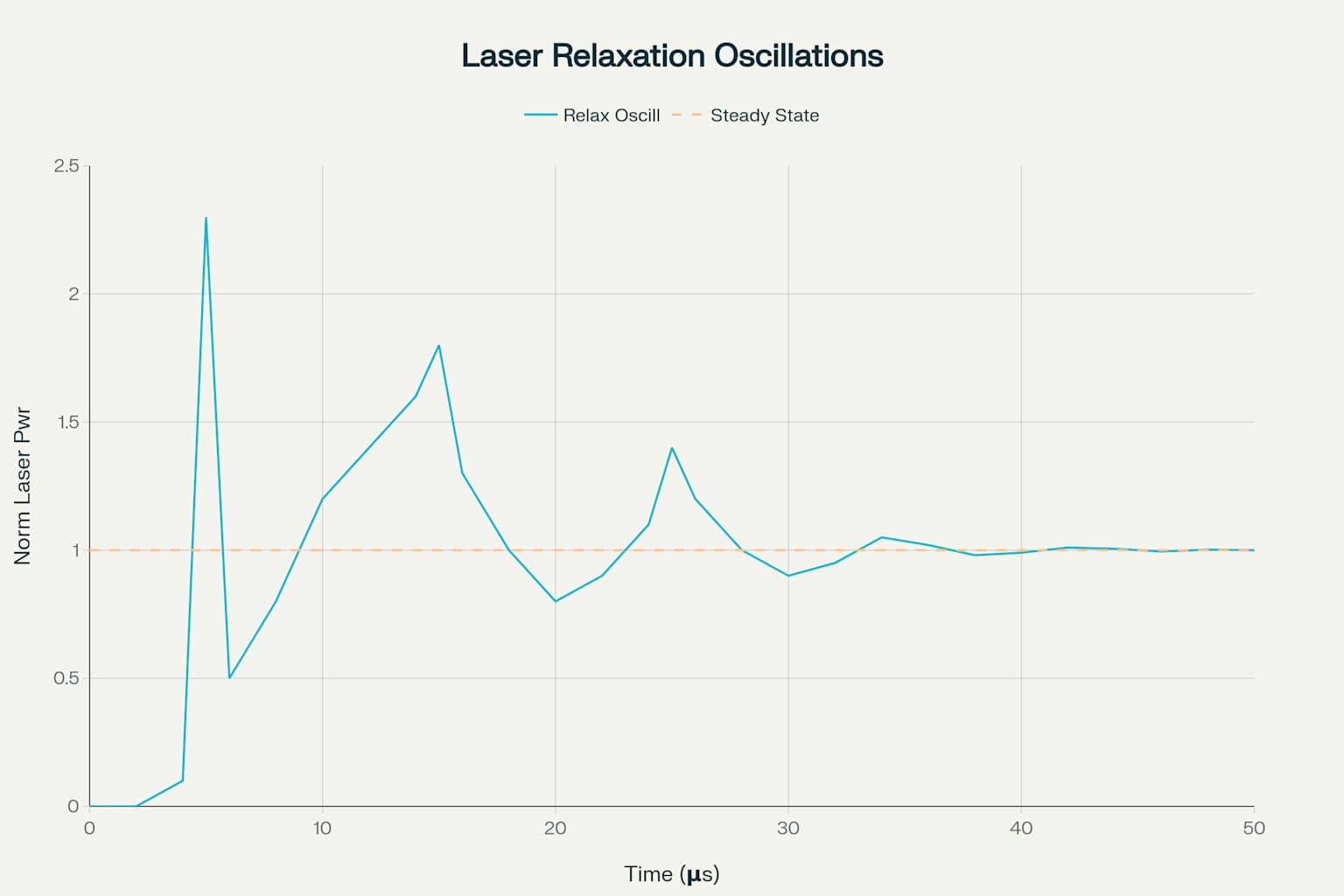
The turn - on dynamics of Class B lasers give some of most dramatic examples of relaxation oscillation phenomena. When pump power is suddenly applied, particularly in solid - state lasers, the output typically shows an series of sharp spikes before settling into damped oscillatory behavior.
The first spike often reaches amplitudes several times steady - state output power and has an duration on order of a few cavity round - trip times. Subsequent spikes become progressively weaker and longer as system approaches equilibrium through exponentially damped oscillations. The temporal spacing between spikes corresponds approximately to inverse of relaxation oscillation frequency.
This spiking behavior is particularly pronounced in three - level laser systems such as ruby lasers, which can show highly irregular and intense spiking patterns. Four - level systems like Nd:YAG typically show more controlled spiking that rapidly evolves into regular damped oscillations.
Accurate measurement of relaxation oscillation parameters gives valuable insights into fundamental laser properties and enables optimization of system performance. Traditional approaches using radio frequency spectrum analyzers work well for lightly damped oscillations but become challenging for heavily damped systems with low signal - to - noise ratios.
Advanced measurement techniques use real - time digital oscilloscopes to capture and average multiple relaxation oscillation events, significantly improving accuracy and precision. These methods can achieve measurement accuracies better than 0.3%, representing substantial improvements over conventional RF spectral analysis.
Relaxation oscillation frequency measurements enable determination of crucial laser parameters including gain cross - sections, saturation energies, and upper - state lifetimes. Such characterization proves essential for laser design optimization and performance prediction.
Understanding and controlling relaxation oscillations has profound implications for numerous applications spanning telecommunications, materials processing, medical diagnostics, and scientific research. In optical communication systems, relaxation oscillations limit modulation bandwidth and contribute to noise characteristics that affect signal quality.
For high - power laser applications, relaxation oscillations can cause beam quality degradation and thermal management challenges. Active stabilization schemes using electronic feedback systems can effectively suppress these oscillations and improve overall laser performance.
In precision applications such as optical metrology and spectroscopy, relaxation oscillation control becomes critical for achieving required stability and accuracy. Modern stabilization techniques can reduce oscillation amplitudes by factors of 50 or more compared to free - running operation.
Contemporary laser systems use sophisticated control strategies to minimize impact of relaxation oscillations on system performance. Active stabilization approaches monitor laser output parameters and apply corrective feedback through various mechanisms including pump power modulation, cavity loss control, and optical injection.
Passive stabilization methods utilize optical feedback from stable reference cavities or nonlinear optical effects to provide inherent stability without electronic control systems. These approaches can be particularly effective for applications requiring ultra - low noise performance.
The development of advanced feedback algorithms and high - bandwidth control electronics continues to push boundaries of achievable stability, enabling new applications in quantum optics, precision metrology, and next - generation optical communication systems.
Research into relaxation oscillation phenomena continues to evolve with development of new laser architectures and applications. Novel approaches including nanostructured gain media, advanced feedback control systems, and hybrid laser - electronic circuits promise to further expand capabilities and applications of controlled laser systems.
The integration of machine learning and artificial intelligence techniques into laser control systems offers unprecedented opportunities for adaptive optimization and real - time performance enhancement. These emerging technologies will likely play increasingly important roles in managing complex laser dynamics and achieving previously unattainable levels of performance and stability.
Relaxation oscillations represent an fundamental aspect of laser physics that profoundly influences performance, stability, and applications of modern laser systems. The distinction between Class A and Class B laser behavior provides essential insights for system design and optimization, while advanced measurement and control techniques enable precise characterization and management of oscillatory phenomena.
As laser technology continues to advance toward higher powers, improved efficiencies, and more demanding applications, mastery of relaxation oscillation physics becomes increasingly critical for developing next - generation optical systems. The comprehensive understanding of these phenomena, combined with sophisticated control methodologies, will enable continued innovation in fields ranging from quantum computing to precision manufacturing and biomedical applications.
Contact: Jason
Phone: +8613337332946
E-mail: [email protected]
Add: Hangzhou City, Zhejiang Province, China